Gadget Inspektor:
Rigol DS2202 Fourier Transformation (Video)
[latexpage]Die Fourier Transformation der Rigol DS 2000er im Video, mit einigen Erläuterungen im Text.
Kein Spektrum Analysator
Natürlich ist ein Oszilloskop kein Spektrum-Analysator und deswegen kann auch die Fourier-Transformations-Funktion eines Oszilloskopes nicht alles bieten, was man sich wünschen würde.
Konkret fehlen der eingebauten Fourier Transformation der Rigol 2000er einige Features, die vielleicht recht nett wären:
- Keine Fourier Transformation mehrerer Kanäle gleichzeitig
- Keine Fourier Transformation eines ausgeschalteten Kanals
- Keine Glättung der Fourier Transformation
- Keine logarithmische Skalierung der Frequenzachse (sehr wohl aber der Signalachse!)
Technische Daten
Die vielleicht wichtigste Frage lautet doch bestimmt: Wie viele Punkte gehen überhaupt in die Fourier Transformation ein?
Zunächst: Speichertiefe und Sample-Rate haben keine direkte Auswirkung auf die Fourier Transformation. Die Fourier Transformation basiert immer auf exakt 1400 Punkten (ja genau! Keine 2er Potenz, also eigentlich wohl eher DFT) und diese 1400 Punkte stammen immer aus dem sichtbaren Bereich der Messkurve. Dadurch sind Frequenz und Auflösung der Fourier Transformation dann auch geklärt:
Frequenz-Limit
Mit einer Auflösung der Zeitachse (Zeit pro Division) von $t_{D}$ ergibt sich eine maximale Frequenz von (Rigol schneidet 20% an dem Ende mit den hohen Frequenzen weg):
\begin{align}
f_{max} = \frac{40}{t_{d}}
\end{align}
[toggle title=“Herleitung“ style=“fancy“]
\begin{align}
f_{sample} = \frac{1400 \ Sa}{t_{d} \cdot 14 \ Divisions}
\end{align}
\begin{align}
f_{max} = \frac{1}{2} f_{sample} * \frac{4}{5} = \frac{40}{t_{d}}
\end{align}
[/toggle]
Auflösung
Für die Auflösung ergibt sich durch die verbleibenden 560 Fourier Transformation-Punkte:
\begin{align}
f_{Auflösung} = \frac{f_{max}}{560 \ \cdot \ t_{D}} = \frac{1}{t_{D} \cdot 14}
\end{align}
Beispiel für Auflösungen und maximale Frequenzen:
Zeitachse maximale Frequenz Auflösung 1 s/Div 40 Hz 0.07 Hz 1 ms/Div 40 kHz 0.07 kHz 1 µs/Div 40 MHz 0.07 MHz
Das Video
Die Beispiele aus dem Video
- Normaler Sinus mit 10 kHz.
- alternierendes Signal mit 5 bzw. 3 Frequenzanteilen.
- Amplitudenmodulierter Sinus 10 kHz mit 1 kHz moduliert.
- Quarzoszillator mit 16 MHz.
- Amplitudenmodulierter Sinus 2 MHz mit 20 kHz moduliert.
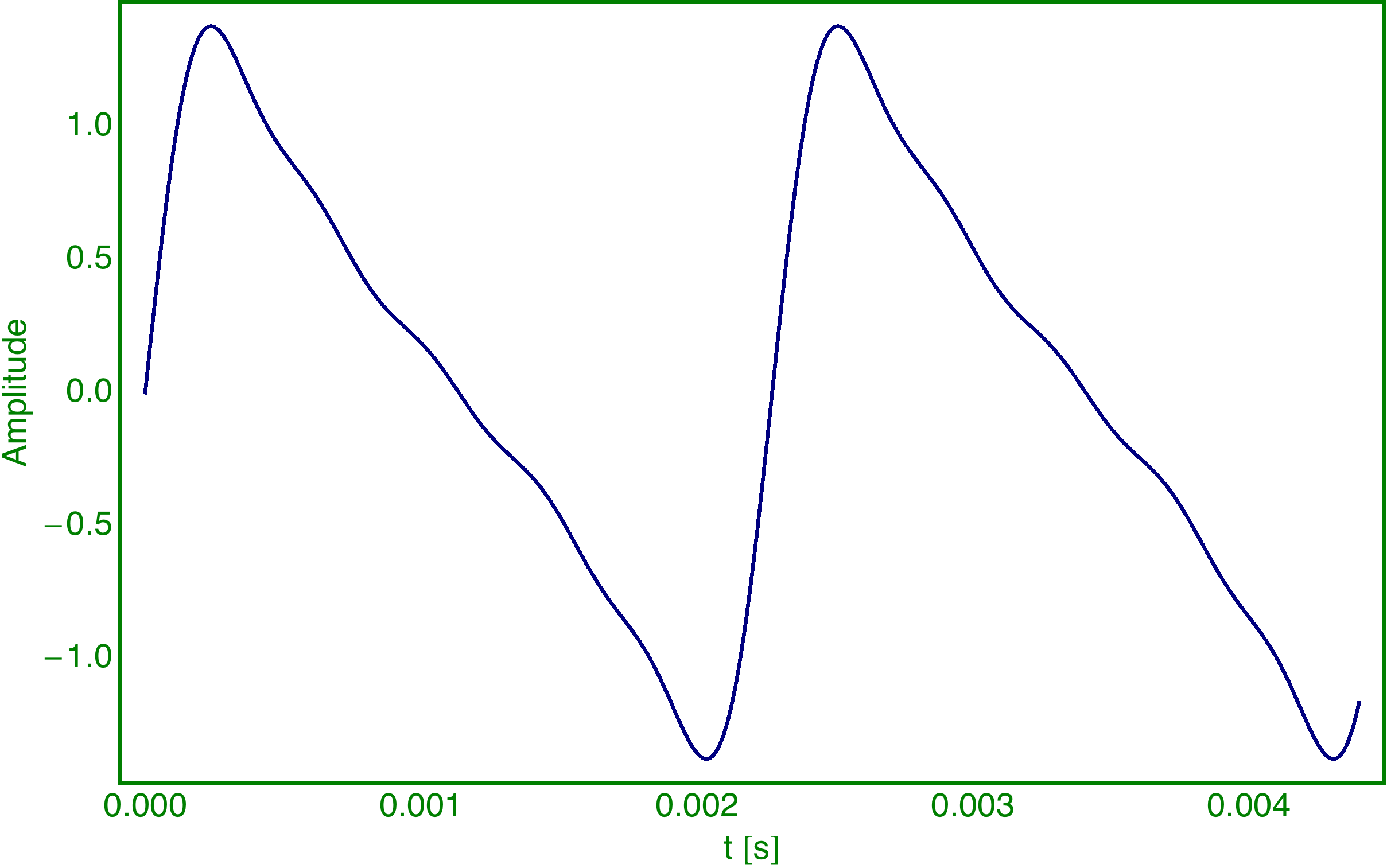
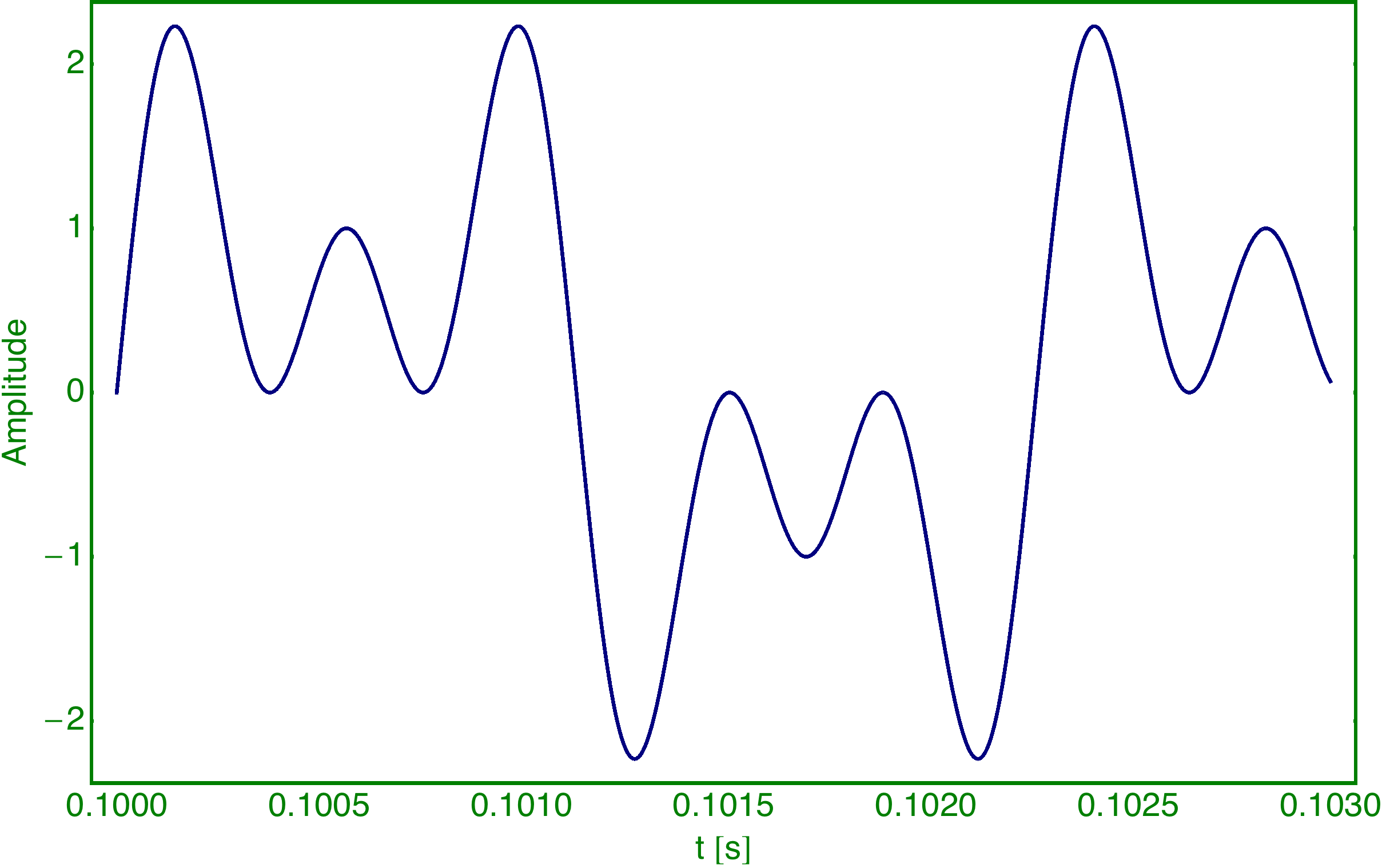
Das alternierende Signal (Details)
Das Signal besteht aus zwei Komponenten, die sich alle 0.1 s abwechseln:
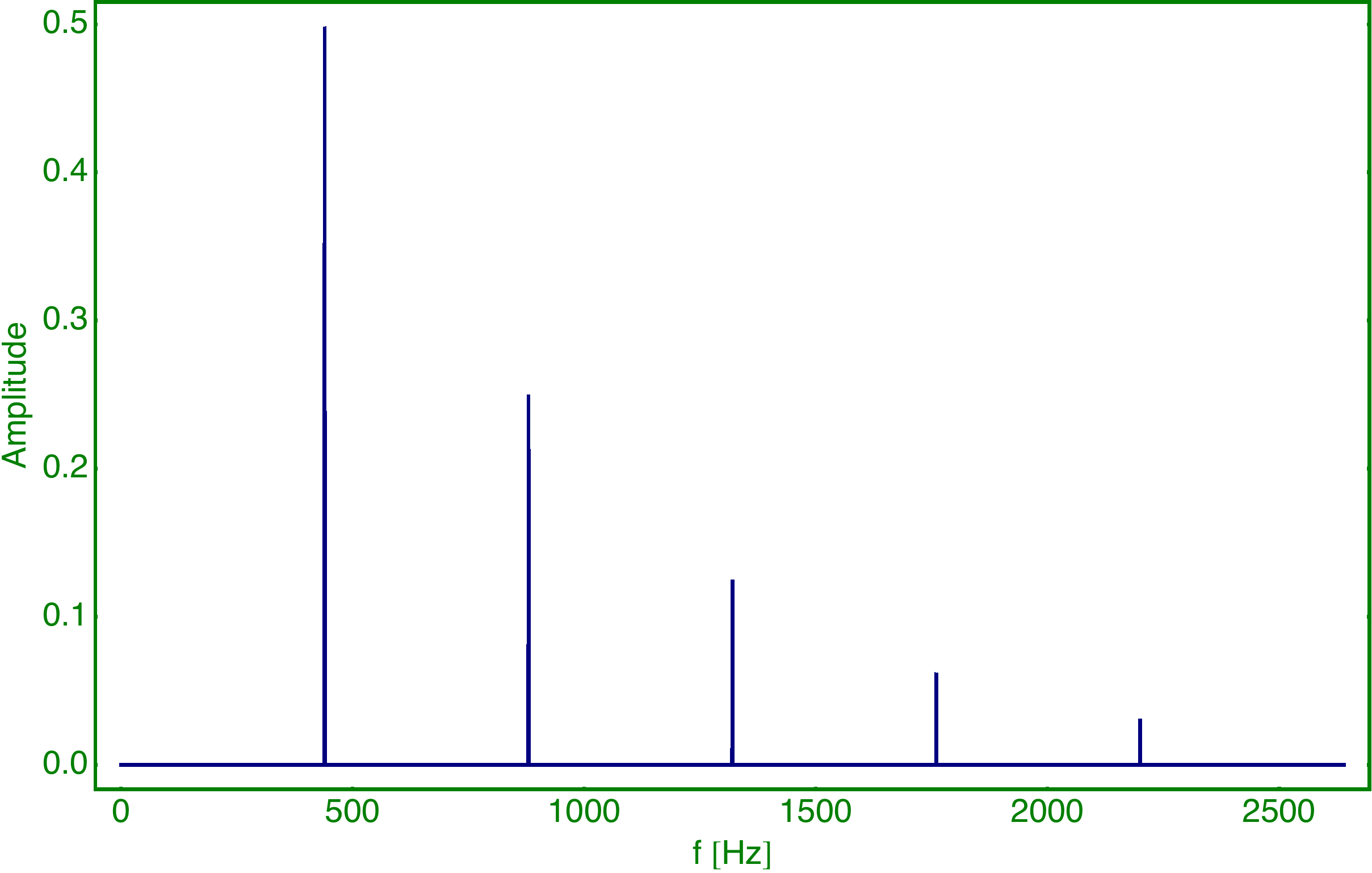
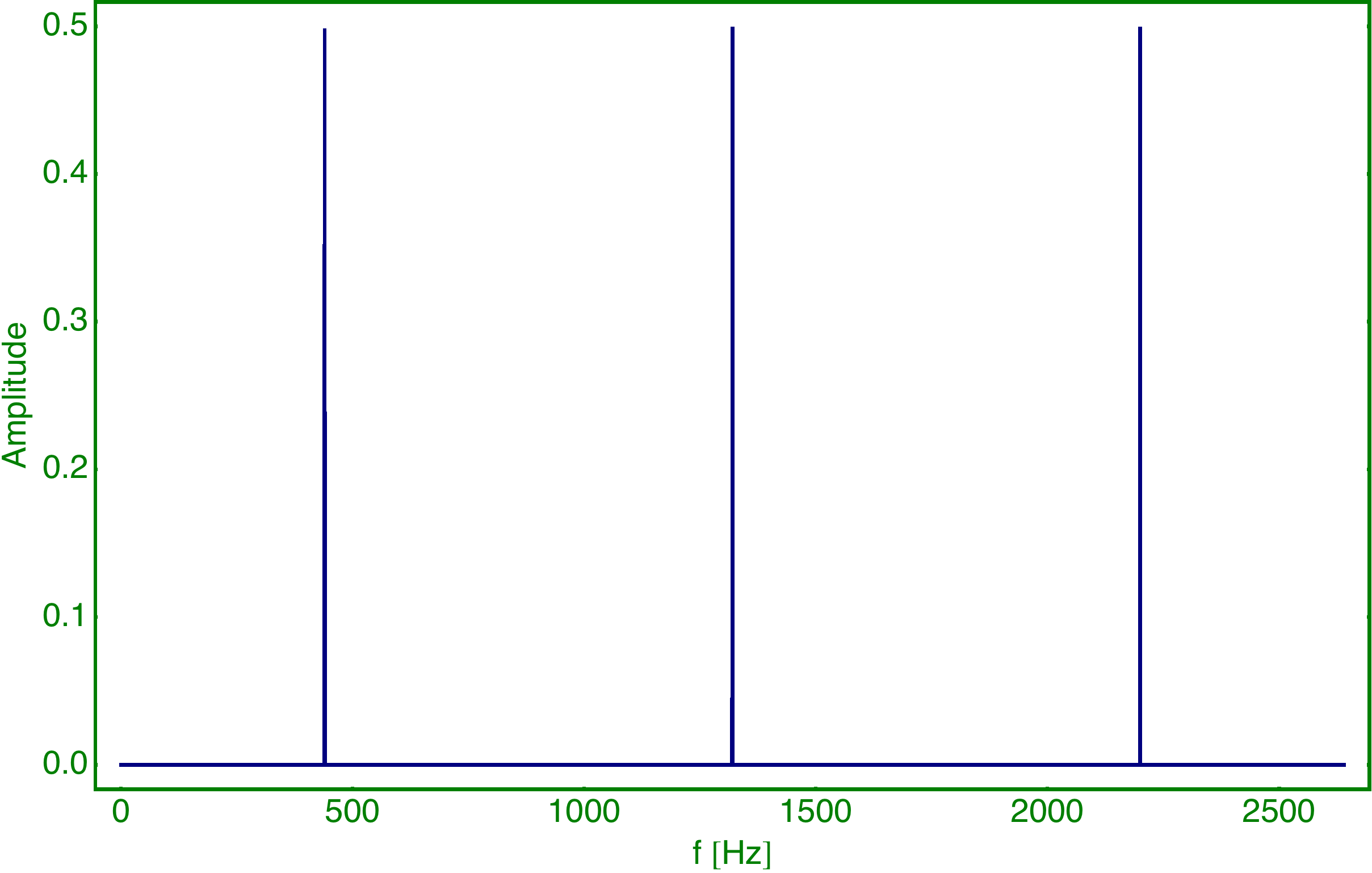
Komponente 1 sieht einem Sägezahn ähnlich und besteht aus: Index Frequenz Amplitude 1 440 Hz 16 2 880 Hz 8 3 1320 Hz 4 4 1760 Hz 2 5 2200 Hz 1
Bei Komponente 2 fehlen die Frequenzen mit den geraden Indizes und alle Amplituden sind gleich groß: Index Frequenz Amplitude 1 440 64 3 1320 64 5 2200 64


Hallo,
zu 1. : du selbst machst den Unterschied zwischen FT und FFT, wie dein Kommentar zuvor zeigt. Wenn du selbst so streng bist in der Verwendung der Terminologie, dann ist deine Aussage falsch.
Die FT ist wie ich schon schrieb, eine zeitkontinuierliche Rechenoperation, ein Integral. Die DFT ist eine zeitdiskrete Rechenoperation, wo das Integral in eine Summe übergeht. Hier wird das zeitkontinuierliche Signal abgetastet, wobei Nyquist eine Rolle spielt.
Die FFT ist die DFT, richtig! Und ganz wichtig: es handelt sich NICHT um eine weitere Transformation, sondern um die Reduktion von Termen der DFT und die Ausnutzung von Symmetrieeffekten! Erst durch diese wird es möglich, ein Spektrum in Sekunden auf modernen FPGAs/DSPs und Controllern zu berechnen, andernfalls hätte man minutenlang kein Bild.
Das alles steht in keinem Widerspruch zu meiner obigen Aussage, dazu braucht es keinen Professor aus Übersee, sondern einfach grundlegendes Wissen über die FT, DFT, FFT, Fourier-Reihe, Nyquist, Abtasttheorem und die praktische Realisierung. Das ist Gegenstand eines jeden Nachrichtentechnikstudiums, erst recht des wissenschaftlichen Studiengangs.
Und enttäuschen muss ich dich leider: auch in angelsächsicher Literatur ist es nicht anders als in der deutschen: es wird sehr genau zwischen FT, DFT, FFT unterschieden, da es gänzlich etwas anderes ist, wenn man diese berechnet!
Da kann ich deinem Professor nur raten, noch einmal das Standardwerk von Alan Oppenheim, Roland Schafer, John Buck zu lesen. Mal abgesehen davon, dass ich sicher mehr als 20 angelsächsische Fachbücher zum Thema besitze, die das auch tun.
2. du machst einen Denkfehler im gesamten Beitrag: die Anzahl der zur DFT/FFT herangezogenen Punkte hat erst einmal NICHTS mit der auf dem Screen angezeigten Anzahl der Punkte zu tun!
Die Herleitung der DFT sieht so aus, dass man ein kontinuierliches Signal abtastet, mit N-Punkten und der Abtastrate T. Daraus ergibt sich das sog. Zeitfenster, dessen Kehrwert die Frequenzauflösung bestimmt, und zwar diskret. Die Anzahl der Bins, also der Frequenzlinien, entspricht nun theoretisch der Anzahl der Abtastpunkte N.
Da eine DFT ca. N^2 – Multiplikationen/Additionen benötigt, käme selbst ein Hochleistungs-FPGA ins Schwitzen. Deshalb verwendet man die FFT, die den Rechenaufwand um viele Potenzen reduziert, ohne dass jedoch das Spektrum schlechter wird! Der Algorithmus von Cooley und Tukey führt dann auf die besagten 2er-Potenzen.
Bis hierher haben wir noch nichts mit den 600 Punkten auf dem Screen zu tun gehabt!
Ein Digiscope hat einen Samplespeicher, in den der ADC schreibt, und einen Bildspeicher, der Daten aus dem Samplespeicher erhält. Wie die 600 Punkte zustandekommen, hängt von der konkreten Implementierung des Algortihmus ab. Oft ist in den billigen Geräten der Speicher so klein, dass nicht mehr genug für die FFT übrigbleibt und die Hersteller dann eben hier zu Kompromissen gezwungen werden. Das ist keine vage Vermutung, sondern Realität.
3. du must dir den Unterschied klarmachen:
die 1000er-Rigols haben ein TFT mit 320 horizontalen Pixeln,
die 2000er-Rigols eines mit 800 horizontalen Pixeln.
Folge: was du siehst, ist entweder stark interpoliert (bei großer Zeitbasis) oder eben die wirklichen Samples (bei kleiner Zeitbasis), wobei du dann nur ein Fenster im Bildspeicher siehst, der Rest ist links und rechts daneben.
Im Frequenzspektrum ist es nun so, dass sie mit den Samples im Samplespeicher die FFT berechnen, beim 2000er ist es eine 2048-Punkte FFT. Idealerweise würden sie nun diese 2048-Punkte auf dem Screen darstellen, dann könntest du dir die Auflösung einfach aus dem Kehrwert des Zeitfensters berechnen. Wenn die von dir genannten 1400 – Frequenzlinien aber nun stimmen sollten, dann haben sie entweder nicht mehr genug Bildspeicher frei, um die kompletten 2048-Punkte darstellen zu können, oder sie haben es sich einfach gemacht, um z.B. die Cursormessfunktionen in Software leichter zu implementieren. Das Geheimnis kennt nur Rigol, und die werden sowas selten offenlegen. Hameg hat es weitaus besser gemacht, und die zeigen die realen FFT-Bins an.
Aber: Rigol gibt selbst in einer Application Note eine 2048er-FFT für die 2er,4er und 6er -Scopes an. Ich habe das 4000er selbst und die FFT ist alles andere als gut gelöst.
Als Entwickler für µC, DSP und FPGA kann ich dir versichern, dass ich weiß, wovon ich spreche.
Dein Artikel muss hinsichtlich der 1400 Punkte nicht falsch sein, aber eine FFT wird auf jeden Fall verwendet, sonst wäre das Gerät überfordert. Wenn du dazu mehr wissen willst, dann wäre das o.g. Fachbuch eine Möglichkeit.
Oder du wartest: ich habe seit einigen Monaten einen Fachartikel in einer bekannten Elektronikzeitung der Industrie. Dieser wird mit mehr Details aber noch woanders veröffentlicht, wo mathematische Zusammenhänge nachvollzogen werden können.
Das Rigol knöpfe ich mir auch noch vor. Ist aber hinsichtlich der FFT eh uninteressant, da sie relativ schlecht im Vergleich zu anderen Geräten ist.
Gruß
Ingenieur NT
(meine Mail klapp momentan nicht, sorry)
FFT durch Fourier-Transformation zu ersetzen, ist falsch. Dabei handelt es sich um eine zeitkontinuierliche Transformation durch ein Integral, welches ein Scope definitiv nicht berechnen kann.
Rigol nutzt wie es überall in der Anleitung steht eine FFT. Wenn man diese mal auf einem FPGA/DSP programmiert hat, dann weiß man, dass eine DFT auch nicht in Frage kommt. Letzter kostet extrem viel Zeit und bringt keinen Vorteil.
Die Aussage mit den 1400 Punkten ist vorsichtig zu behandeln. Rigol selbst gibt per Application Note für alle Geräte eine 2048 FFT an. Diese kann man auf ein Display natürlich umskalieren.
Dann ist es noch eine ganz andere Sache, ob der Support immer alles richtig versteht, was Entwickler versuchen zu erklären. Oft kommt dann etwas anderes heraus, als es den Tatsachen entspricht.
Rigol macht eine FFT, auch nach eigenen Aussagen. Die FFT der Rigols ist aber alles andere als gut gelungen, da gibt es weitaus bessere Scopes mit FFT-Analyzer, die besser auflösen und freie Wahl der Punkte zulassen.
Hallo,
1. die Auffassung eine FFT sei keine FT ist abwegig. Vielleicht ist das in Ingenieur-Deutschland so üblich, da mag ich nicht mitreden, aber ich habe extra einen befreundeten Mathe-Prof in den Staaten angemailt und er hat mir bestätigt, was die Sprache eh schon nahelegt: FFT ist eine spezielle DFT und selbstverständlich ebenso wie eine analytische FT eine FT. Wie der Name schon andeutet. Natürlich ist auch ein schnelles Auto ein Auto, ebenso wie ein diskretes Auto, das Gleiche gilt auch für die schnelle Fourier Transformation. Falsch geht anders.
2. Für die 1000er gibt Rigol ausschließlich und konsistent 600 Punkte an, das kann keine FFT sein. Trotzdem nennt Rigol es FFT. Der Grund ist klar, weil man umgangssprachlich eben jede numerische FT als FFT bezeichnet, auch wenn das nicht exakt stimmt. Also nochmal: Bei den 1000ern 600 Punkte, keine FFT.
3. Dann rechne doch mal vor! Kann ja sein, dass die die 1400 Datenpunkte in ein 2048er FFT-FPGA stecken, aber wieso sollte Rigol die Auflösung der Transformation dann nachträglich so krumm runterrechnen? Dafür gibt es keinen vernünftigen Grund. Die von mir angegebenen Auflösungen sind ja am Bildschirm abgelesen, dann rechne doch gerne mal vor, wie die mit 2048 Punkten zustande kommen, dann schreibe ich gerne und zügig den ganzen Artikel um!
Natürlich kann das alles bei einem 2000A wieder anders sein, das hat ja eh ein paar andere Eigenschaften.
Vlg
Dr.S.van Hay
Hi,
ich finde auch die Erklärungen zur FFT super , vielen Dank!
P.S. Stimmt das denn mit den 1400 Punkten, das ist ja keine 2er Potenz?
Hi,
ich habe das mal zu Anlass genommen, überall FFT durch Fourier Transformation zu ersetzen. Streng genommen wäre es ja dann keine FFT. Ich habe keine Ahnung, ob es 1400 Punkte sind, die Zahl stammt aus einer Mail von Rigol. Klar ist, dass es nicht unbedingt eine 2er Potenz sein muss, denn Rigol hat ja auch beim 1052 keine 2er Potenz verwendet, sondern 600 Punkte (?).
Hi,
klasse Video-Quali und sehr interessant. Habe mir kürzlich den DS2072 zugelegt und zum 2202 mit allen Optionen gepimt (wie, dürfte bekannt sein). Durch dieses Video konnte ich einiges, neues lernen, besten Dank.
Hi,
schön, dass dir das Video gefällt!