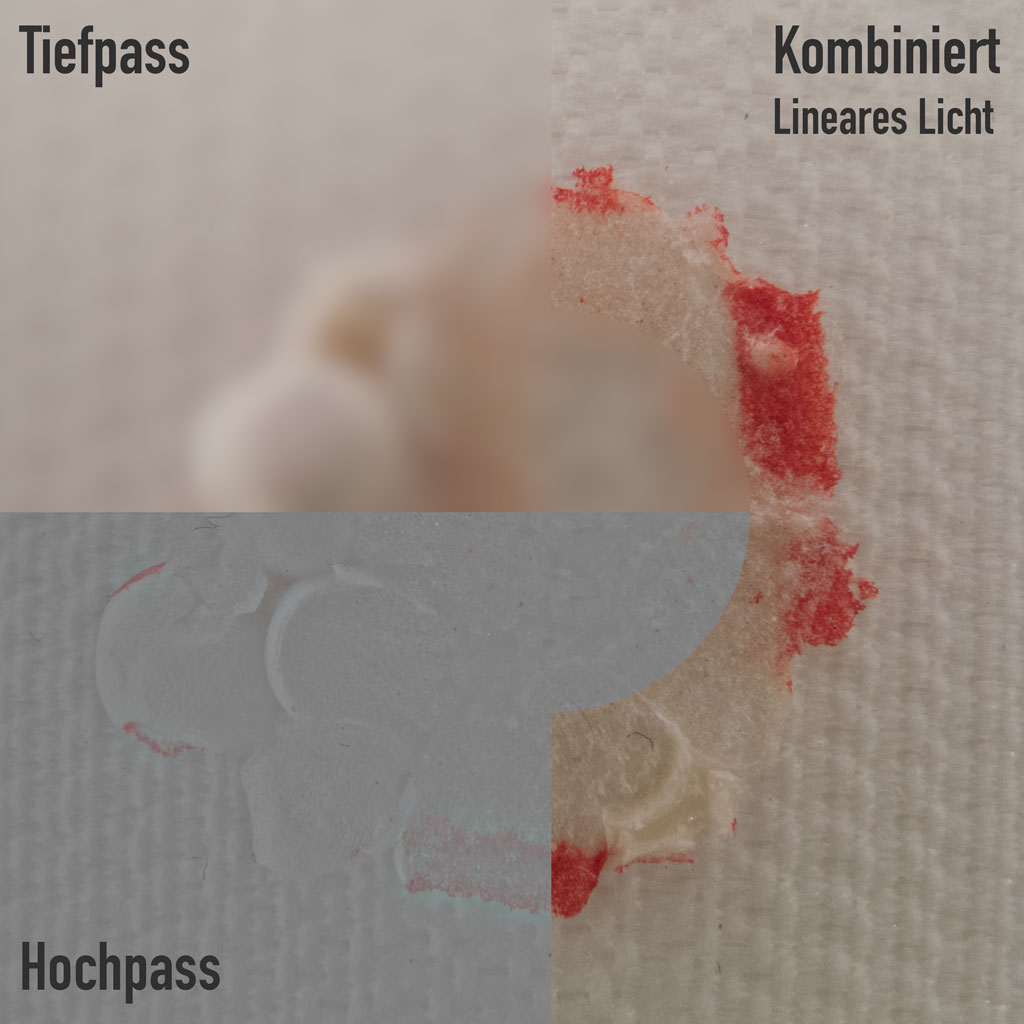
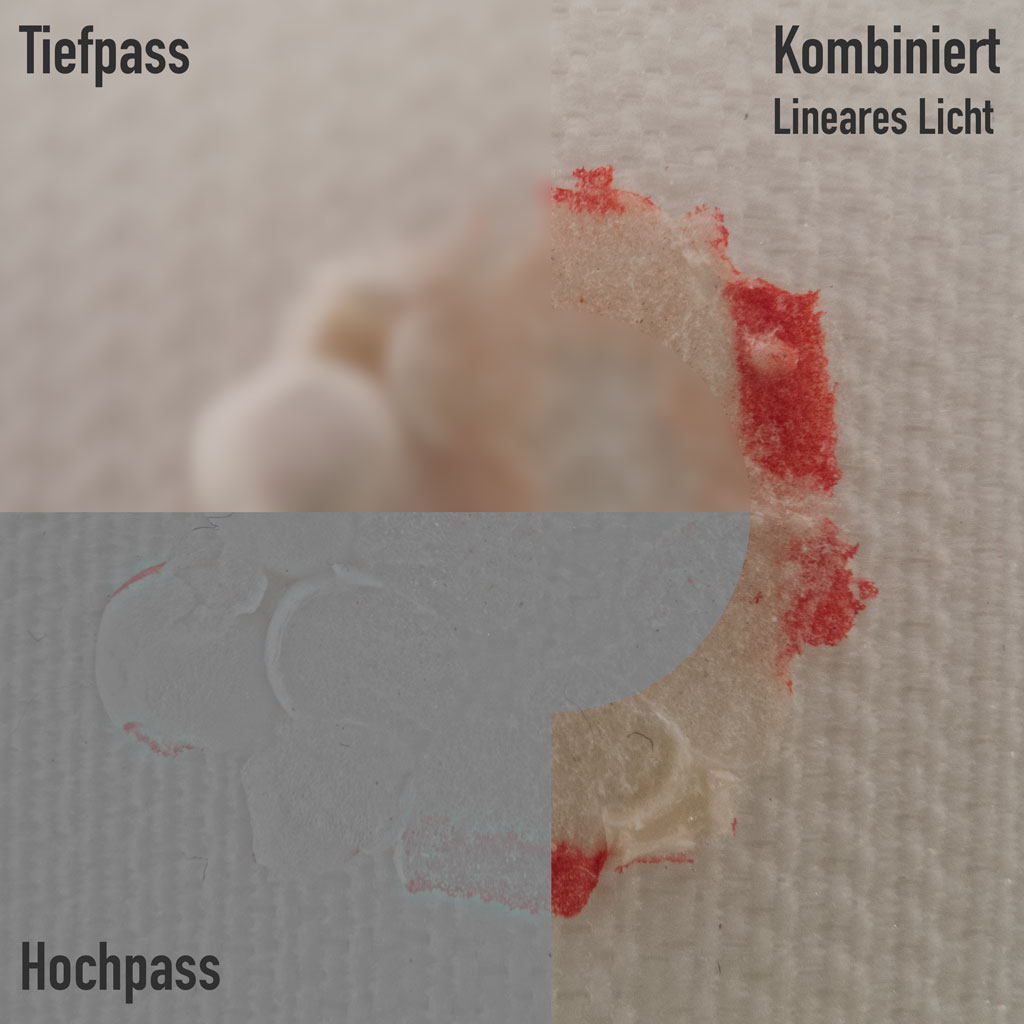
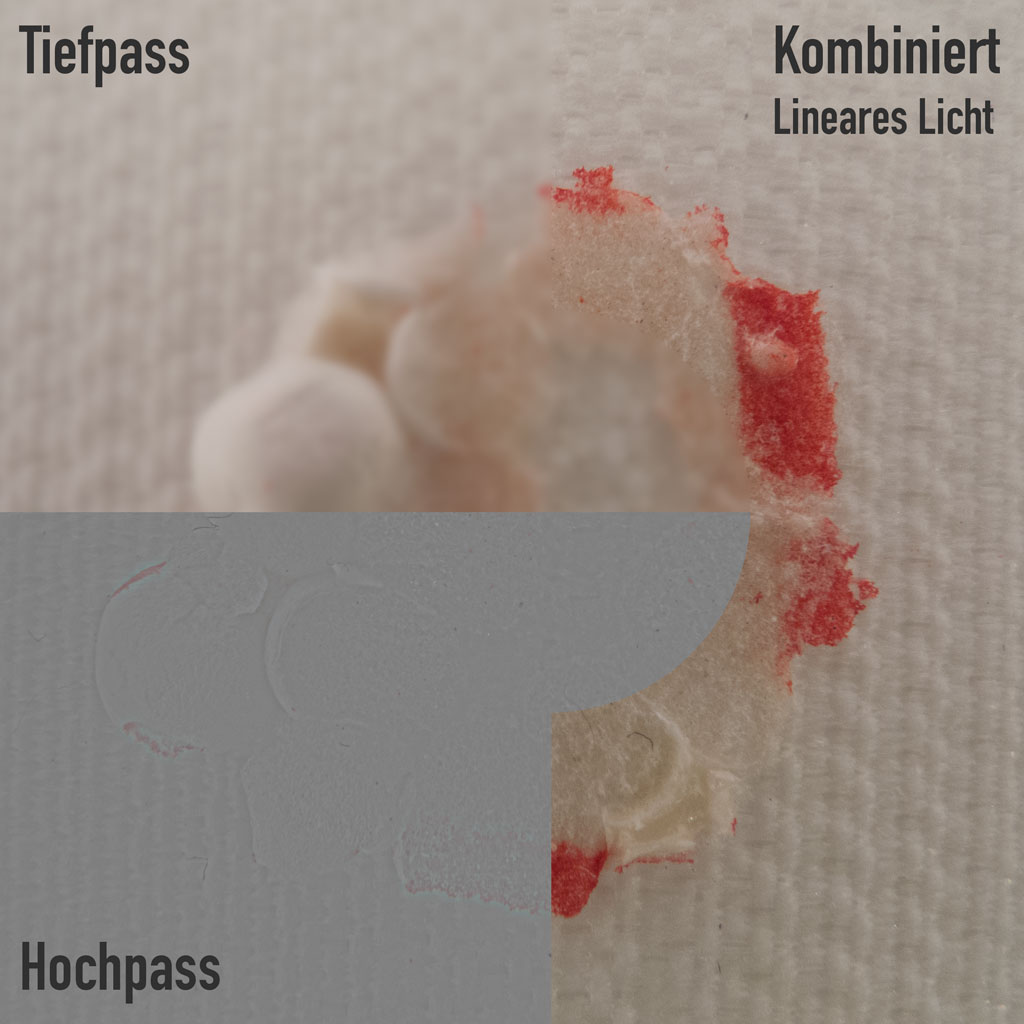
Wie funktioniert der Hochpass?
[latexpage] Photoshop Hochpass in Fourier-Analyse und Ablauf für die Split-Frequency Separation.
Allgemeines
Aus der Elektronik kennt man den Tiefpass als eine Kombination aus Widerstand und Kondensator, die tiefe Frequenzen durchlässt und hohe Frequenzen abschwächt.
So ähnlich ist das bei Photoshop auch gemeint. Unter hohen Frequenzen werden dabei scharfe Pixelübergänge verstanden und unter niedrigen Frequenzen weiche Übergänge.
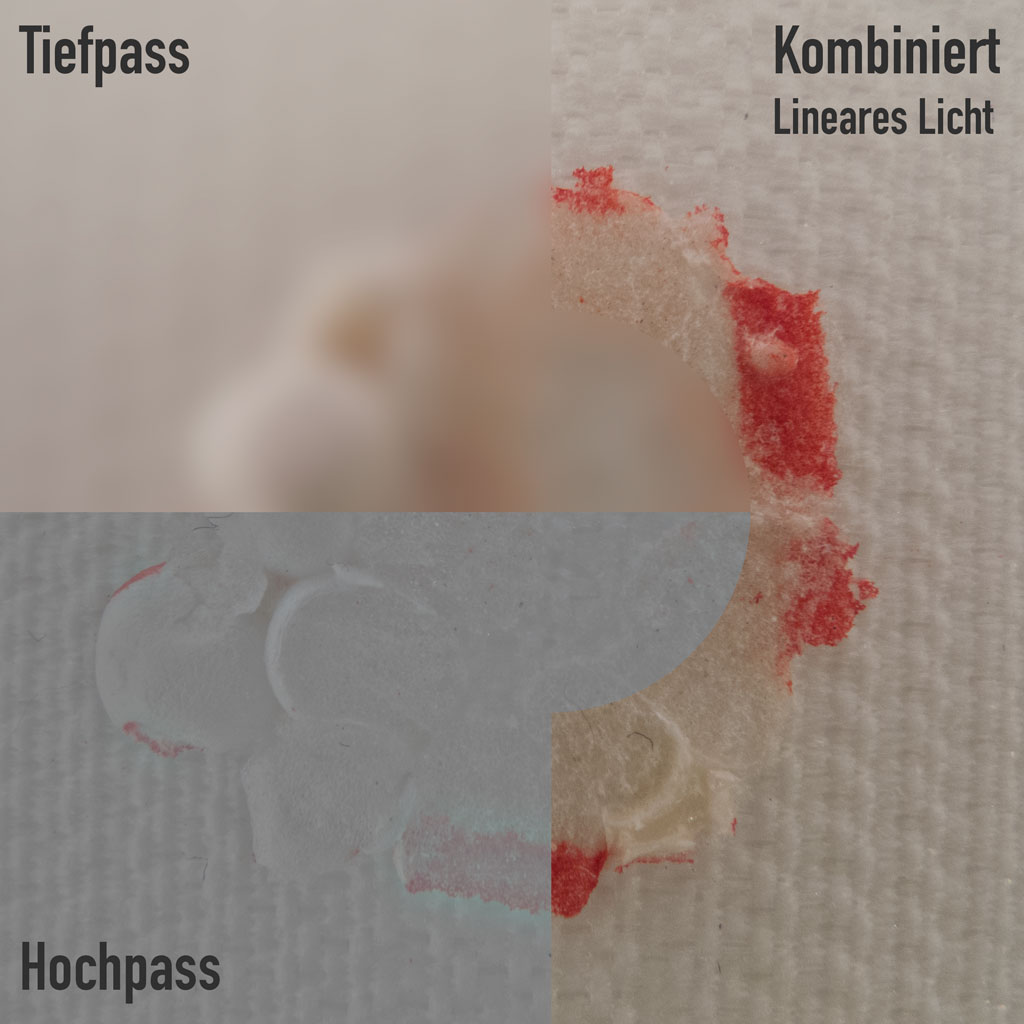
Damit ist auch schon klar, wie ein Tiefpass aussieht: Tiefpass ist der Gaussche Weichzeichner. Unter Hochpass-Filtern scheint „man” im Allgemeinen das Anwenden des Gausschen Weichzeichners und das Abziehen der Weichzeichnung vom Original zu verstehen (Beziehungsweise einen Filter, der das selbe Ergebnis liefert, wie dieser Vorgang).
An diesem Beispielbild habe ich mir diesen Vorgang mal Schritt für Schritt genau zur Brust genommen und zum Beispiel jeweils in einer Fourier-Analyse angeschaut . Also, hier das Originalbild:
Das Bild hat eigentlich keine Besonderheiten, insgesamt ist es ein sehr weißes Bild und wegen der schlechten Lichtverhältnisse etwas verrauscht, was man so in der Darstellung kaum sieht. Sehr interessant ist die Gewebestruktur im Hintergrund, die ich mir in Zukunft noch genauer anschauen will und die in der Nachbearbeitung sicherlich noch etwas herausgearbeitet werden sollte.
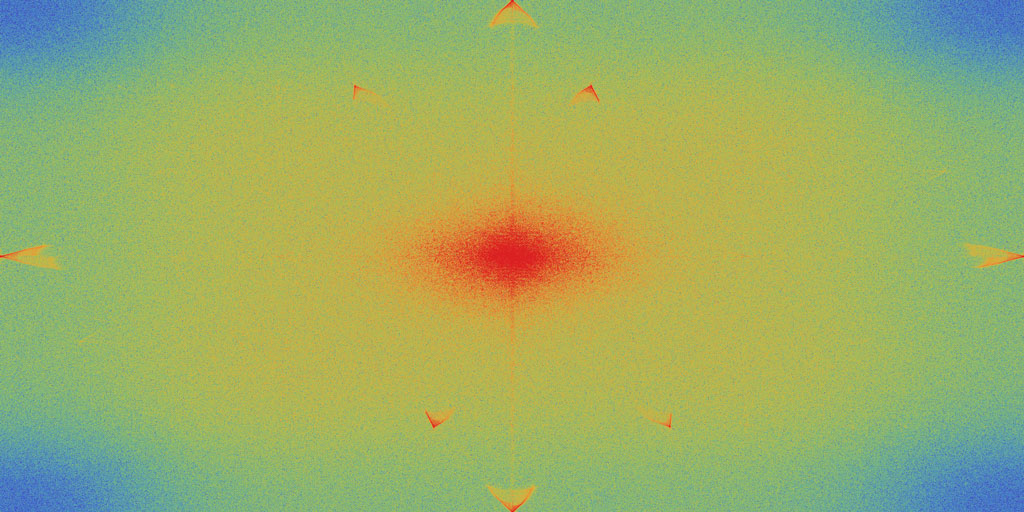
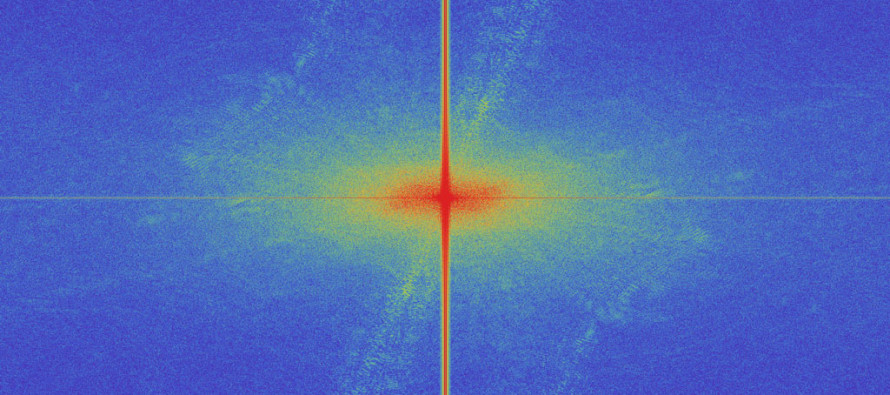
So sieht die Darstellung der zugehörigen Fourier-Analyse aus:
Die hübschen Pfeilspitzen bei den höchsten Frequenzen kommen vom Rauschen der Kamera. In der Bildmitte sind die niedrigen Frequenzen angeordnet, achte auf den senkrechten Strich in der Bildmitte, der wird sich sicherlich im Hochpass am deutlichsten verändern. Ansonsten wird die Abbildung erst im Vergleich mit den anderen Frequenzsspektren interessant.
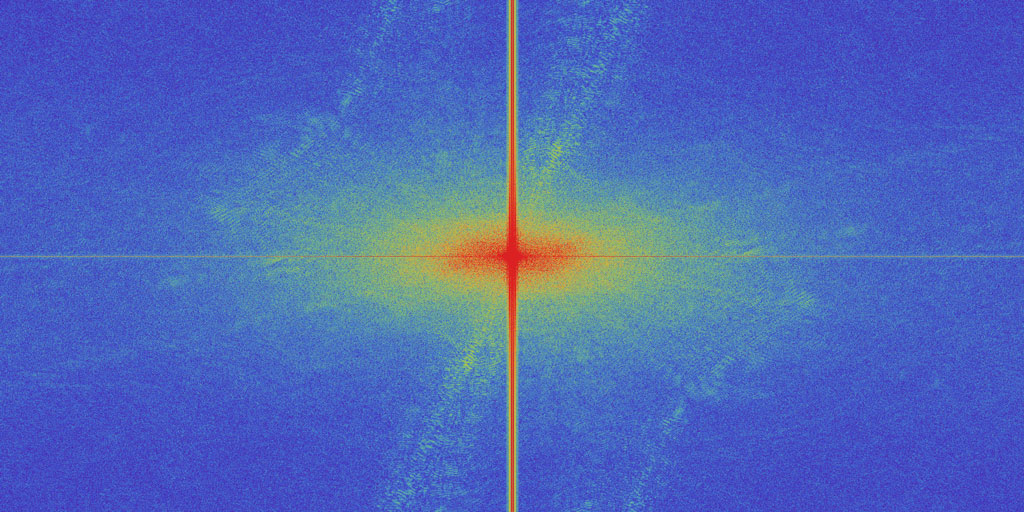
Hier das Frequenzspektrum nach Anwendung des gausschen Weichzeichners (Foto weiter unten):
Du erkennst sofort, dass dieses Frequenzspektrum zu einem Tiefpass gehört. Der senkrechte Strich ist sehr viel deutlicher geworden, der waagerechte Strich ist überhaupt erst sichtbar geworden und in den mittleren Frequenzen ist viel mehr Struktur erkennbar als vorher, weil die hohen Frequenzanteile, die diese Bereiche bisher überdeckt haben verschwunden sind.
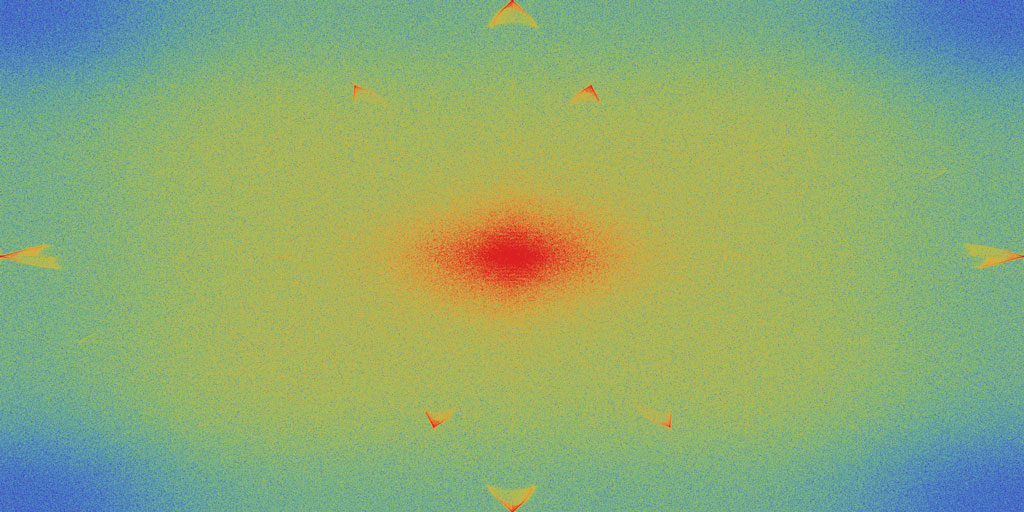
Wenig überraschend ist das Ergebnis, wenn ich diese beiden Spektren nun voneinander abziehe (Foto weiter unten):
praktisch das gesamte Rauschen ist im Hochpass-gefilterten Teil, du siehst auch, dass die senkrechte Linie komplett verschwunden ist, was auch nicht so verwunderlich ist, schließlich liegen in der Mitte die niedrigen Frequenzen.
Ich wollte nur zeigen, dass mit Hochpass und Tiefpass tatsächlich ein Verhalten ähnlich „richtigen” (komische Ausdrucksweise) Hochpass- oder Tiefpass-Filters gemeint ist.
Für die Bildbearbeitung eröffnen sich natürlich interessante Möglichkeiten, wenn man ein Bild bei gleichem Aussehen in ein hochfrequentes Bild und ein niederfrequentes Bild aufteilen kann und die beiden Anteile separat mit normalen Bildbearbeitungswerkzeugen bearbeiten kann.
Ein – wie ich finde – beeindruckendes Beispiel folgt bald!
Photoshop Workflow
Naja, Gausschen Weichzeichner brauche ich wohl nicht erwähnen, trotzdem der komplette Ablauf. Aus irgendeinem Grund wuseln im Internet verschiedene Abläufe für 16-Bit und für 8-Bit Bilder herum. Warum? Wäre schön, wenn mir das jemand erklären würde! Dieser Workflow funktioniert jedenfalls mit 16 Bit und mit 8 Bit Werten.
Der Anfang ist immer gleich:
- Ebene duplizieren
- Auf die untere Ebene den Gausschen Weichzeichner anwenden (z.B. mit 40 px)
- Die obere Ebene auswählen
- Bild -> Bildberechnungen aufrufen
Tiefpass vom Original abziehen = Hochpass (Version für „16 Bit” (geht genauso mit 8 Bit))
- Quelle: die untere Ebene, Haken bei „Umkehren”
Mischmodus: Addieren
Skalieren: 2
Versatz: 0
Das Ende ist immer gleich:
- Mischmodus der oberen Ebene auf „Lineares Licht” setzen um Tiefpass und Hochpass für die Anzeige zu verschmelzen.